有一段代码是利用高斯函数来做曲线拟合的,比较简单和方便,调试起来可能也会简单些。首先利用高斯函数生成0~256之间的sigma为75的曲线,第一个点按照1024归一化。大致如下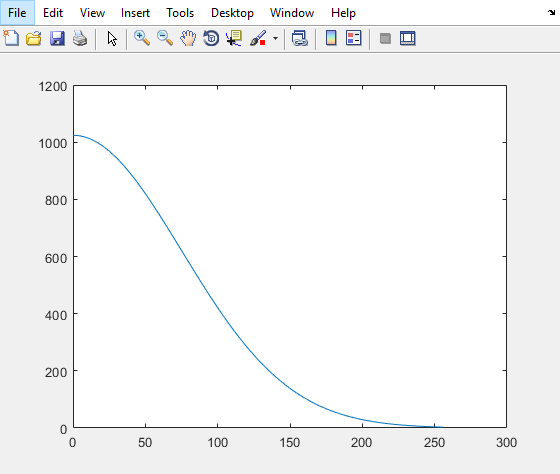
然后利用标准正太分布公式来计算给定sigma和mean的高斯曲线。
|
clr; |
有一段代码是利用高斯函数来做曲线拟合的,比较简单和方便,调试起来可能也会简单些。首先利用高斯函数生成0~256之间的sigma为75的曲线,第一个点按照1024归一化。大致如下
然后利用标准正太分布公式来计算给定sigma和mean的高斯曲线。
#define _CRT_SECURE_NO_WARNINGS |
clr; |