A Tutorial Introduction to the Lambda Calculus

Posted on | Edited on | Views:
Symbols count in article: 8k | Reading time ≈ 7 mins.

参考文献

这里以第二篇开始lambda演算的学习
λ演算是一种形式系统(formal system)，什么是形式系统呢？大家都知道，数学语言是可以脱离现实而存在的——大家把数学想成了一种符号游戏，脱离生活常识，从公理开始，进行大量的推导和证明——最终产生了一个系统，在这个系统中有公理、定理、推论、猜想……这种自成系统，有公理又承认推理证明方法的体系，成为形式系统。而用于描述形式系统的语言就是形式语言(formal language)

图灵完备

首先先理解一下什么是图灵完备，参考知乎的答案# 什么是图灵完备？

什么是图灵机

图灵机是图灵在1936年发表的paper中提出的数学模型，是一个架空概念，他在文中描述了什么是图灵机，并且证明，只要图灵机可以被实现，就可以用来解决任何可计算问题。
图灵机的结构包括：

  1. 一个无限长的纸带
  2. 一个字符表
  3. 一个读写头
  4. 一个状态寄存器
  5. 一个有限的指令集

图灵机可以解决什么问题

图灵证明，假设上述模型所说的功能都可以被某种形式物理实现，那么任何可计算问题都可以被解决。
所谓可计算问题，涉及到计算理论（即泛指一切与计算相关的问题），可以理解为，是否存在一个算法，能解决在任何输入下的此计算问题，比如著名的停机问题，就是一个不可计算的计算问题。
简单所，图灵证明了对于一个问题，对于任何输入，只要人类可以保证算出结果，那么图灵机就可以保证计算结果。

什么是图灵完备性

图灵完备性，是针对一套数据操作规则而言的概念，数据操作规则可以是一门编程语言，也可以是计算机里的实现的指令集。当这套规则可以实现图灵机模型里的全部功能时，就称为具备图灵完备性。

直观理解图灵完备——Brainfuck语言

1993年，有人发明了Brainfuck语言，只有8个有效字符，每个字符都是一个指令，但这却是一门图形完备的编程语言。
BF的工作机制与图灵机基本一致，他存储数据的方式是一个无限长的一位整数数组，里面的数值全部初始化为0，还有一个数据指针，每个时刻都指向数组的某一元素，指针可以左右移动，也可以读取、修改数组当前元素的值。
BF中8个有效字符分别是：

- >
指针向右移动一格
- <
指针向左移动一格
- +
使指针当前格数值加一
- -
使指针当前格数值减一
- .
把当前格数值按 ASCII 表输出到终端
- ,
从终端接受一 byte 的数据，存储其 ASCII 数值到当前格
- [
当指针当前值为 0 时，程序跳转至与之对应的 ] 之后；否则程序正常执行
- ]
程序跳转回与之对应的 [ 处

+++++
[
>+++++++++++++
<-
]
>.

对于上述代码段，通过完成5X13输出了字符A,
这里讲一下我的理解，+进行五次，因此当前指针初始化的格子cell 0的值被递增了5次
[指令读取到当前值各自值为5（因此将[]中的部分执行了5次，[]中的程序会递减该值，直到0），来看[]中的行为
>右移指针，随后将当前指针的各自cell 1递增了13次，再左移一个到cell 0，将cell 0的值递减一次
随后>.右移指针并将当前值格子cell 1的值打印出来，得到A

图灵停机问题

不存在有这样一个程序，能够计算任何程序在给定的输入上是否会结束（停机）。
用反证法，假设有这样一个程序，叫做GodAlg，给定一个程序，并且给定这个程序的输入，就能够判定这个程序在这个输入上是否会停机。

bool GodAlg(char *program, char *input) {
    if (<program> halts on <input>)
        return true;
    return false;
}

我们假设一个新的程序

bool SatanAlg(char *program) {
    if (GodAlg(program, program)) {
        while (1);
        return false;
    }
    return true;
}

当这个算法调用自身时，SatanAlg(SatanAlg)会产生的结果如何？
从代码片段来看，这个程序要么能够结束运行停机，要不不能返回。

  1. 假设能够停机，则if判断成立，程序进入循环，于是这个调用永远不会返回，说明SatanAlg(SatanAlg)不能停机。
  2. 假设不能够停机，则返回true，说明SatanAlg(SatanAlg)能停机。
    这说明假设不成立，不存在这样的一个程序GodAlg

λ演算

定义

λ演算被称为最小通用编程语言，1930年由Church引入，用于公式化有效计算中的一些问题，它也是图灵完备的，但更强调变换规则的使用，而不是具体的实现，并且其约束的规则非常简单，易于演算。
λ演算中只有三种表达式，分别如下。在λ演算中，只有λ和.是关键字。

- <expression>  := <name> | <function> | <application>
- <function>    := λ <name>.<expression>
- <application> := <expression><expression>

注意表达式可以是name，function和application，对于，在λ演算中，只有λ和.是关键字！
记住最后一个表达式，两个expression表示application。对于表达式，默认是从左到右进行分析或者应用应用的。

最简单的恒等函数为

函数可以应用于表达式，例如下式表示将函数应用到$y$上

关于function application可以通过替换规则替换body中的argument实现求值，例如

这里$[y/x]$表示将所有的$x$替换为$y$
λ演算中有α transform和β reduction，在λ演算中，变量是没有任何含义的，不代表任何东西，只是用先相同的名字表示两个相同的东西。而函数也什么都不计算，就是一个表达式，唯一能做的就是β规约(β reduction)，直到没有任何东西可以再替换为为止。

  • α transform
    对于λ演算中的任何表达式，可以修改函数参数的名称，只要同时修改函数体的内所有的引用。（替换有约束变量的名字）
  • β reduction
    指的是，对于一个application，可以将函数体中和对应函数标识符相关的部分做替换来实现application，方法就是使用标识符作为参数值替换，也就是下面的substituions部分。（将实参应用到函数体中）

约束变量(bound variable)和自由变量(free variable variable)


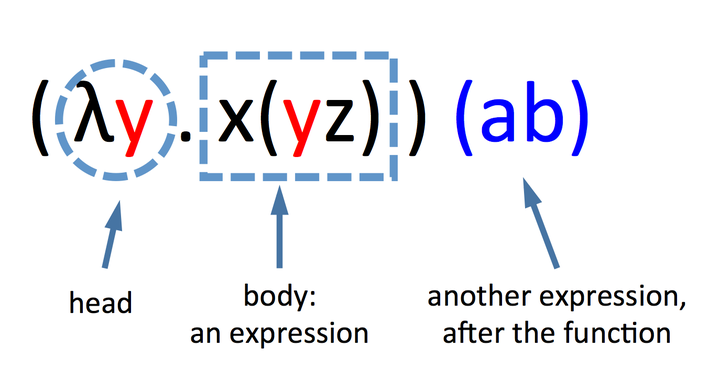
在头部(head)中提及的变量被成为约束变量，没有提到的成为自由变量，因为函数可以是其他函数的一部分，所以一个变量可以同时是约束变量，又是自由变量。

substitutions

由于在λ演算中当要使用一个函数时，都需要完整写出完整的定义，这里可以使用其他字符来代替定义，例如恒等function

当恒等function应用于本身时，可以表示为

注意前后的$x$是互相独立的，上式可以写作

对上式作变量替换，将所有$x$用$\lambda z.z$替换

算术

λ演算最早就是应用于算术运算的，但在λ演算中只有函数，并没有所谓的数字，这里用丘齐数来表示，首先定义zero，然后one用suc(zero)表示，two用suc(suc(zero))表示。
zero表示为，需要接受两个参数s和z

可以简写为（λ演算中只定义了单个参数的函数，但是多个参数的函数无非就是单个函数的多次调用，其实就是柯里化）

简化后的式子可以接受两个参数，第一个可替换s，第二个可替换z。这个表达式被应用时，会把第一个表达式丢掉，然后第二个原封不动。
利用这个记号法，其他自然数可以定义为

以上的计数法其实就是在z之上嵌套表达式s，数字多大就嵌套多少次，就是对z应用了n次s。这其实就是自然数的本质，不断加1。
我们定义后继函数(successor function)如下

后继函数可以应用于0得到

同理可以得到2等等，由此即可得到加法的定义，例如2+3就表示2S3，即2 suc 3次。注意以下推导中，2接受两个参数S和3，分别将S和3作为s和z替换，同时也要注意到$S3=4$

柯里化(currying)

这一块可以参考wiki的解释。柯里化就是把接受多个参数的函数变成接受一个单一函数（最初函数的第一个参数）的函数，并返回接受剩余参数的函数的新函数的技术。

举个例子很典型

add(3, 5) -> add(3)(5)

0的定义为$\lambda sz.z$，这个其实是$\lambda s.(\lambda z.z)$是完全等价的。

乘法(multiplication)

例如2x2的结果为如下，注意2是可以接受两个参数的，所以$2s(z)$实际上是2接受了$s$和$z$作为输入，得到s(s(z))

时刻要记住每个应用函数时，接受了几个参数，并且是左结合的。

条件(conditionals)

定义以下两个函数为真和加，分别接受两个参数返回其中的一个，真就返回第一个，假就返回第二个

逻辑运算(logical operations)

例如

条件测试(a conditional test)

定义一个函数，如果参数是数字0则返回T，否则返回F

验证如下，注意0表示接受两个参数，然后用第一个参数对第二个参数作用0次

注意到，F对任何参数的应用都是返回恒等函数

因此，上式继续展开为

另外可以换一种方式理解，$\mathrm N \mathrm F \lnot \mathrm F $同时也表示对对$\lnot $应用n次$\mathrm F$，然后结果再应用于$\mathrm F $。注意到$\mathrm F $的定义，接受两个参数，仅仅返回第二个参数。第一个$\mathrm F $实际接受了两个参数，一个是对$\lnot$应用了n-1次F的返回值，另一个是后面的一个$\mathrm F $，因此抹掉第一个参数返回第二个参数，也就是返回最后面的那个$\mathrm F $，也就是最后就返回$\mathrm F $。

前继函数(predecessor function)

对于n的前继，通用的做法是创建一个序对(pair)，(n,n-1)然后返回需对的第二个参数作为结果。序对用λ演算可以表示为

将该函数应用于$\mathrm T$就可以返回序对的第一个数

同理，应用于$\mathrm F$就可以返回需对的第二个数

利用下面这个函数就可以由序对(n,n-1)生成(n+1,n-1)

这里感觉应该是由序对(n,n-1)生成(n+1,n)才对啊！

注意一下对上式的理解，在函数体z(S(pT))(pT))中，如果没有对z进行规约，则该式子不会进行任何计算；如果用数字n对z进行规约，变成n(S(pT))(pT)，此时才可以进一步进行参数替换S(pT)作为n的第一个参数，pT作为第二个参数。

其中，子表达式$pT$从序对p中提取第一个元素。上式会构造一个新的序对，第一个元素是原序对第一个元素的后继——S(pT)，第二个元素就是第原序对的第一个元素——pT。

简单来说，应该是由序对(a,b)生成(a+1,a)。

因此n的前继就是应用n次$\Theta$到序对$\lambda z.z00$（得到(n,n-1)）然后返回第二个参数得到n-1：

可以我们可以进行推导

以此类推。同时要注意到$P0=0$，该性质对其他函数的定义很有用，验证如下

相等与不等

定义如下函数判断数字$x$是否大于等于$y$

这里的$xPy$表示对y应用x次的前继，也就是y-x，如果该式等于0，说明$y \le x$。
利用$x \ge y$与$y \ge x$同时成立表示$x=y$，可以得到下面这个关于相等的定义

用同样的方式我们也可以定义$xy$和$x\neq y$。

递归

在λ演算中，递归函数可以定义为调用函数y并且返回自身

注意这里其实是加括号了，完整表示如下

这里第二个$(\lambda x.y(xx))$是规约到第一个约束变量x中去的还是不会减少表达式的个数，
该函数应用于R时

考虑从0到n的求和函数R

该函数对n进行了测试，如果n为0的话，就返回0；如果n不为0则返回n+(r(n-1))，这里r其实是对自身函数的调用。这里我们怎么知道r是对自身的递归调用呢？在λ演算中我们没有对函数定义名字的。这就是给出递归操作Y的原因，例如求和到3

这就是Y组合子(Y combinator)!

0%